Sammanfattning av nationella provet i matte 1

Nationella proven i matte 1 består av tre skriftliga delprov. Alla inriktningar har mycket gemensamt, men det som gör matte 1b unikt är att kursen inkluderar funktionsförståelse, olikheter och sannolikhet. Matte 1c inkluderar dessutom rätvinkliga trianglar och vektorer. Här har vi samlat allt du behöver veta inför nationella provet i matte 1!

/Fredrik Fridlund på Allakando

Sammanfattning av nationella provet i matte 1

Tal

Räknelagar

Prioriteringsregler

I uttryck med flera räknesätt beräknas uttrycket i följande ordning:

Parenteser
Potenser
Multiplikation och division
Addition och subtraktion

Exempel: $5 + 3 \cdot 2 (6-2)$

$\quad =5 + 3 \cdot 2(\mathbf{4})$
$\quad =5 + 3 \cdot \mathbf{8}$
$\quad =5 + \mathbf{24} = 29$

Negativa tal

Två lika tecken ger plus och två olika tecken ger minus

+ + ger + – – ger +

+ – ger – – + ger –

Bråk

Ett bråk består av:

\frac{\text{T\"aljare}}{\text{N\"amnare}} = \text{kvot}

Förlängning

Vid förlängning multipliceras nämnare och täljare med samma tal.

Addition & subtraktion

Samma nämnare
Lägg ihop täljarna

Exempel: Vad är $\frac{4}{3} + \frac{5}{2}$ ?

Svar: För att få gemensamma nämnare får vi förlänga $4/3$ med $\color{#3396C9}2$ , och $5/2$ med ${\color{#96C933} 3}$ .

\frac{4}{3} + \frac{5}{2} = \frac{4 \cdot {\color{#3396C9} 2} }{3 \cdot {\color{#3396C9} 2}} + \frac{5 \cdot {\color{#96C933} 3}}{2 \cdot {\color{#96C933} 3}} = \frac{8}{6} + \frac{15}{6} = \frac{8 + 15}{6} = \frac{23}{6}

Multiplikation

Multipliceras nämnare med nämnare och täljare med täljare.

\frac{8}{3} \cdot \frac{5}{7} = \frac{8 \cdot 5}{3 \cdot 7} = \frac{40}{21}

Division

Multiplicerar täljaren med nämnarens inverterade värde.

Exempel: Lös ekvationen $\frac{4x - 6}{7} = 2$ .

Multiplicera med 7 på båda sidor: $\quad\frac{4x-6}{\color{red}\cancel{\color{#96C933} 7} } \cdot {\color{red} \cancel{\color{#96C933} 7} } = 2 \cdot {\color{#96C933} 7}$ ‎

Addera 6 på båda sidor: $\quad 4x - {\color{red} \cancel{\color{black} 6 }} {\color{#96C933} + } {\color{red} \cancel{\color{#96C933} 6 }} = 14 {\color{#96C933} + 6 }$ ‎

Dividerar båda sidor med 4: $\quad\frac{{\color{red} \cancel{\color{black} 4 }} x}{ \color{red} \cancel{\color{#96C933} 4 }} = \frac{20}{\color{red} \cancel{\color{#96C933} 4 }}$ ‎

Svar: $\quad x=5$

Inverterade värdet innebär att nämnaren och täljaren har bytt plats

\frac{3}{7} \rightarrow \frac{7}{3} \qquad \frac{4}{9} \rightarrow \frac{9}{4}

Potenser

En potens består aven bas och en exponent.

Potenslagar

$a^x \cdot a^y = a^{x+y}$	$(a^x)^y = a^{xy}$	$\frac{a^x}{a^y} = a^{x-y}$
$\left( \frac{a}{b} \right)^x = \frac{a^x}{b^x}$	$\frac{1}{a^x} = a^{-x}$	$a^0 = 1$

Obs! För att kunna använda potenslagarna måste vi ha samma bas.

Ekvationer

Förstagradsekvationer

Om du ska lösa en ekvation måste du få x‐variabeln ensam på ena sidan av likhetstecknet. För att göra detta kan du använda dig av de fyra räknesätten. Du kan använda dem hur du vill bara du gör exakt samma sak på båda sidor.

Plus på båda sidor $x - 5 = 9$ $x - 5 {\color{#96C933} + 5 } = 9 {\color{#96C933} + 5 }$ $x = 14$	Minus på båda sidor $x + 7 = 18$ $x + 7 {\color{#96C933} - 7} = 18 {\color{#96C933} -7 }$ $x = 11$
Dela på båda sidor $3x = 21$ $\frac{3x}{\color{#96C933} 3 } = \frac{21}{\color{#96C933} 3}$ $x = 7$	Multiplicera båda sidor $\frac{x}{2} = 9$ $\frac{{\color{#96C933} 2 \cdot } x}{2} = {\color{#96C933} 2 \cdot } 9$ $x = 18$

Exempel: Lös ekvationen $\frac{4x - 6}{7} = 2$ .

Multiplicera med 7 på båda sidor:

Addera 6 på båda sidor:

Dividerar båda sidor med 4:

Svar:

$\frac{4x-6}{\color{red}\cancel{\color{#96C933} 7} } \cdot {\color{red} \cancel{\color{#96C933} 7} } = 2 \cdot {\color{#96C933} 7}$ ‎

$4x - {\color{red} \cancel{\color{black} 6 }} {\color{#96C933} + } {\color{red} \cancel{\color{#96C933} 6 }} = 14 {\color{#96C933} + 6 }$ ‎

$\frac{{\color{red} \cancel{\color{black} 4 }} x}{ \color{red} \cancel{\color{#96C933} 4 }} = \frac{20}{\color{red} \cancel{\color{#96C933} 4 }}$ ‎

x=5

Potensekvationer

Innebär att x är upphöjt med ett tal.

T.ex. $x^5 = 243$

Målet är att få x:et fritt. För att få x:et fritt höjer man upp båda sidor med exponentens inverterade värde.

Exempel: $x^5 = 243$ ‎

$(x^5)^{1/5} = 243^{1/5}$ ‎

$x^{5 \cdot \frac{1}{5}} = 243^{1/5}$ ‎

x^1 = 3

Svar: $x=3$

$x^n = C$ ‎

x = C^{1/n}

Kom ihåg:

Vid en potensekvation höjer man upp båda sidor med exponentens inverterade värde
Om det är en jämn exponent finns det en negativ och en positiv lösning.
Om det är en udda exponent finns det bara en lösning.

Procent

Procent betyder hundradel.

När man räknar med procent kan man använda sig av en triangel för att använda rätt formel.

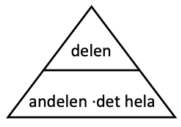
Inom procent finns det tre basproblem

1. Hur stor är delen?

$12 \% \text{ av } 3000 =$ ‎
$= 0,12 \cdot 3000 = 360$

$\text{delen} = \text{andelen} \cdot \text{det hela}$

2. Hur många procent är delen av det hela?

Hur mycket är 14 av 25?
$\frac{14}{25} = 0,56 = 56 \%$

$\frac{\text{delen}}{\text{det hela}} = \text{andelen}$

3. Hur stor del av det hela?

15 % av ett tal är 300. Vilket är talet?
$\frac{300}{0,15} = 2000$

$\frac{\text{delen}}{\text{andelen}} = \text{det hela}$

Förändringsfaktor

Förändringsfaktor används för att ta fram det nya värdet vid en procentuell förändring direkt.

Ökning med 20 %. Nytt värde: $100 \% + 20\% = 120\%$ .
Förändringsfaktorn $= 1,2$ .
Minskning med 20 %. Nytt värde: $100 \% - 20\% = 80\%$ .
Förändringsfaktorn $= 0,8$ .

$\text{uspv} \cdot \text{ff} = \text{nytt v\"arde}$
‎

Exempel: En cd‐spelare kostar 300 kr. Priset ökar med 12 %. Vad är det nya priset?

$\text{Ursprungsv\"arde} = 300 k$ ‎

$\text{F\"or\"andringsfaktor} = 1 + 0,12 = 1,12$ ‎

$\text{Nytt v\"arde} = 300 \cdot 1,12 = 336$ ‎

Svar: 336 kr.

Index

Ett index visar hur priser förändras över en tid. När man sätter upp ett index väljer man ett år som man utgår ifrån. Detta år kallas för basår. Basåret har alltid indexvärdet 100.

Exempel: Tabellen nedan visar hur priserna för en vara har förändrats under perioden 1990 ‐ 2010.

a) Hur har priserna förändrats mellan 1990 och 2010?

b) Hur har priserna förändrats mellan 2005 och 1995?

År	Pris	FF	Index
$1990$	$30\;kr$	$1,00$	$100$
$1995$	$34\;kr$	$34/30 \approx 1,13$	$113$
$2000$	$41\;kr$	$41/30 \approx 1,37$	$137$
$2005$	$49\;kr$	$49/30 \approx 1,63$	$163$
$2010$	$55\;kr$	$55/30 \approx 1,83$	$183$

Svar:

a) $\frac{183}{100} = 1,83 \rightarrow +83%$ . Stigit med 83%
b) $\frac{144}{100} \approx 1,44 \rightarrow +44%$ . Stigit med 44%

Funktioner

Formler & uttryck

Ett algebraiskt uttryck innebär att man har en eller flera bokstäver, variabler, som man kan byta ut med olika värden.

Endast rörligt värde

Exempel: Ken köper ris som kostar 12 kr/kg.

Kostnaden kan beskrivas med uttrycket

$y = 12x$ .

Då vi inte har något fast värde är priset vi betalar direkt proportionellt mot mängden ris Ken köper. Om Ken inte köper något ris behöver han inte betala något.

Rörligt och fast värde

Exempel: Att gå på ett tivoli kostar 200 kr i inträde. Om man ska åka karuseller kostar det sedan 50 kr per åktur.

Kostnaden kan beskrivas med uttryck

y = 50x + 200

Det fasta värdet innebär att även om vi inte åker någon karusell kostar det fortfarande 200 kr i inträde, bara för att komma in på tivolit.

Linjära funktioner

Linjära funktioner består oftast av ett rörligt och ett fast värde. Det rörliga värdet är det som står bredvid variabeln, och det fasta värdet är det som står ensamt.

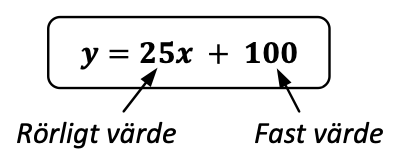
Det rörliga värdet kallas för $k-v\"arde$ och det fasta för $m-v\"arde$ . Den allmänna formeln är: $y = kx+ m$ .

Värdena beräknas enligt följande:

$k = \text{r\"orligt v\"arde} = \frac{\text{skillnad i } y}{\text{skillnad i } x}$
$m = \text{startv\"arde} \rightarrow \text{testa!}$

När man arbetar med linjära funktioner arbetar man
antingen med grafer och textuppgifter.

Grafer

Exempel: Grafen nedan visar kostnaden för att anlita en snickare x timmar. Sätt upp en funktion för kostnaden.

Svar: Vi ska ställa upp en funktion med ett rörligt och ett fast värde.

Det rörliga värdet är så mycket som grafen förändras när x ökar med ett.

När $x = 0$ är $y = 200$ . När $x = 2$ är $y = 500$ . Det innebär att $y$ har ökat med 300 då $x$ ökar med 2.

Om $x$ ökar med 1 ökar alltså $y$ med $\frac{300}{2} = 150$

Rörliga värdet $= 150$

Det fasta värdet är där grafen skär y-axeln.

Fast värde $= 200$

Svar: Funktionen är $y = 150x + 200$

Exponentialfunktioner

Exponentialfunktioner är funktioner där vi har en variabel som exponent.

Geometri

Formler för areor och volymer finns på formelbladet så dem behöver man inte lära sig utantill. När man använder en formel byter man ut bokstäverna mot de siffror man fått.

Här är ett exempel:

Exempel: Beräkna volymen för en kon med diametern 12 cm och höjden 18 cm.

Vi tar fram volymformeln för en kon från formelbladet:

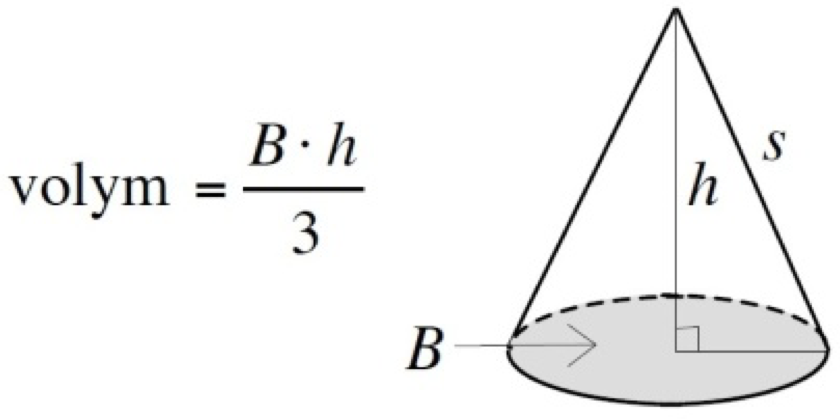
Basarean B beräknas som arean för en cirkel; $\pi \cdot r^2$ . Radien är halva diametern; 6 cm. $B = \pi \cdot 6^2 \approx 113$

Nu vet vi att ${\color{#96C933} B =133}$ och ${\color{#3396C9} h = 18}$ , så nu kan vi använda volymformeln:

$\text{Volym } = \frac{{\color{#96C933} B} \cdot {\color{#3396C9} h}}{3} = \frac{{\color{#96C933} 113} \cdot {\color{#3396C9} 18}}{3} = 678 \; cm^3$ ‎

Svar: Volymen för konen är $678 \; cm^3$

Vinklar

Trigonometri

Det finns tre trigonometriska samband man jobbar med:

$\sin v = \frac{a}{c}$
$\cos v = \frac{b}{c}$
$\tan v = \frac{a}{b}$

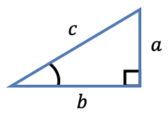
När man jobbar med trigonometri räknar man antingen ut en sträcka eller en vinkel.

Skala

Areaskala = (längdskala) $^2$

Volymskala = (längdskala) $^3$

Vektorer

En vektor är en storhet som har både storlek och riktning.

Koordinatform: $\vec v = (x_v, y_v)\qquad$ Vektorns längd: $|\vec v| = \sqrt{x_v^2 + y_v^2}$

Vid addition och subtraktion av vektorer lägger man ihop deras x‐komposanter för sig och deras y‐komposanter för sig.

Addition

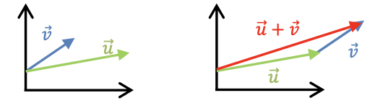
$\vec u + \vec v = (x_u, y_u) + (x_v, y_v) = (x_u + x_v, y_u + y_v)$ ‎

Subtraktion

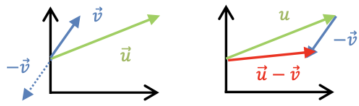
$\vec u - \vec v = (x_u, y_u) - (x_v, y_v) = (x_u - x_v, y_u - y_v)$ ‎

Multiplikation med skalär

$k \cdot \vec v = k(x_v, y_v) = (kx_v, ky_v)$ ‎

Statistik & Sannolikhetslära

Lägesmått

Det finns tre typer av lägesmått man ska kunna:

$\mathbf{\text{Medelv\"arde}} = \frac{\text{summan av alla v\"arden}}{\text{antalet v\"arden}}$
$\mathbf{\text{Median}} = \text{mittenv\"ardet i en talf\"oljd (i storleksordning)}$
$\mathbf{\text{Typev\"arde}} = \text{v\"ardet som f\"orekommer flest g\aa nger}$

Statistik
På de nationella proven är det vanligt att det kommer minst en uppgift som innebär att du ska tolka ett diagram; avläsa något ur det. Däremot krävs inte kunskapen att kunna rita ett avancerat diagram själv.

Följande diagramtyper ska kunna tolkas:

Stapeldiagram
Linjediagram
Cirkeldiagram
Histogram

Felkällor

När man granskar statistik är det viktigt att vara kritisk och inte lita blint på siffrorna. Det finns många olika felkällor, och man kan även manipulera diagram så att de blir missvisande.

De vanligaste felkällorna är följande:

Mätfel – Mätningen gjordes felaktigt
Urvalsfel – Man tog inte hänsyn till variationer imålgruppen.
Bortfall – Det var många som inte svarade påenkäten.

Sannolikhetslära

Sannolikheten för händelsen A betecknas $P(A)$

P(A) = \frac{\text{antalet g\aa nger A intr\"affade}}{\text{antalet m\"ojliga utfall}}

En sannolikhet kan anges i bråkform, decimalform eller i procent.

Komplementhändelsen till A är sannolikheten att A inte inträffar. Denna beräknas genom

P("\text{inte } A") = 1- P(A)

Oberoende händelser

Följande regel gäller för oberoende händelser i flera steg. Sannolikheten av att båda händelserna ska inträffa får du om du multiplicerar de båda händelsernas sannolikheter med varandra.

P(A \text{ och } B) = P(A) \cdot P(B)

Diagram för två tärningar

Ett vanligt problem inom sannolikhetslära är kast med två tärningar. För att lösa dessa problem använder man sig att ett speciellt diagram.

Ett diagram för två tärningar ritas enligt nedan:

Varje axel står för en tärnings resultat.

Beroende händelser

Om två händelser inte kan inträffa samtidigt är sannolikheten för att någon av händelserna kommer att inträffa lika med summan av sannolikheterna för de båda händelserna.

Exempel: Om sannolikheten för att en skytt ska missa sitt mål är 0,3 och sannolikheten för att han ska träffa är 0,7 är sannolikheten att han antingen träffar eller missar
0,3 + 0,7 = 1