Omkrets
Omkretsen av en figur är längden av alla figurens sidor tillsammans. Omkrets anger vi i enheterna millimeter (mm), centimeter (cm), decimeter (dm) och meter (m). Sambandet mellan enheterna ser ut som följande:
1000 mm = 100 cm = 1 dm = 1m
För att ta reda på omkretsen behöver vi veta måtten av figurens sidor. Måtten får vi genom att mäta i figuren med vår linjal. Vi mäter alltså varje sida, och så fort vi är färdiga med en sida skriver vi upp måttet bredvid sidan. Sedan adderar (plussar) vi längderna av alla sidor, vilket ger oss omkretsen.
I vissa fall anges dock figurens mått i uppgiften. Då behöver vi alltså inte mäta i figuren, utan vi adderar längderna direkt.
Så räknar du ut omkretsen
Låt oss säga att vi vill mäta omkretsen av följande triangel. Vi ska svara i centimeter (cm).

Det finns inga utritade mått i figuren och därför vet vi att vi ska mäta sidorna själva. Vi mäter längden av sidorna och får:
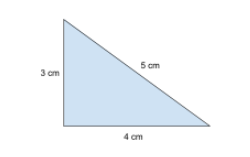
För att räkna ut omkretsen adderar vi längden av alla sidor.
3+4+5=12\;cmVi får att triangelns omkrets är 12 cm.
Ofta när vi vill räkna ut omkretsen av en rektangel är endast två sidor utmarkerade i uppgiften. Det är då viktigt att komma ihåg att motsatta sidor alltid har samma längd.
När vi räknar ut omkretsen av en sådan rektangel börjar vi alltid med att markera ut längden av sidorna där måtten inte står. Sedan adderar vi längderna av sidorna på vanligt vis för att få omkretsen.
Låt oss säga att vi har en rektangel med mått enligt figuren. Vi vill beräkna omkretsen och vi ska svara i meter (m).
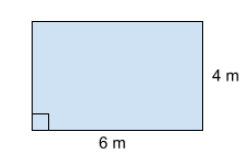
Vi börjar med att markera ut längden av de tomma sidorna. Sidorna är lika stora som den motsatta sidan.
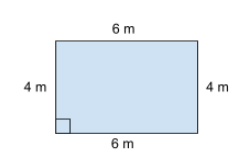
Nu har vi hittat längden av alla sidor. Då kan vi addera sidlängderna för att få omkretsen.
4+6+4+6=20\;mVi får att rektangelns omkrets är 20 m.
I vissa fall kan vi behöva räkna ut längden av figurens sida då vi redan vet omkretsen.
Säg att vi har en kvadrat med omkretsen 8 dm. Vi vill beräkna längden av kvadratens sida. Vi ska svara i decimeter (dm).
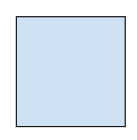
I en kvadrat är varje sida lika lång. Vi vet alltså att 4 sidor ger den sammanlagda längden 8 dm. Med andra ord har vi att sidans längd multiplicerat med 4 blir 8 dm:
{sidan}\cdot{4}=8Då vi vill beräkna värdet av “sidan” vill vi att det ska stå ensamt om likamedtecknet. Därför delar vi nu båda sidorna med 4. Det gör så att fyran hoppar över till den högra sidan, eftersom fyrorna på den vänstra sidan av likamedtecknet tar ut varandra.
{sidan}\cdot{4}=8 \frac{{sidan}\cdot{4}}{4}=\frac{8}{4} sidan=\frac{8}{4}Vi dividerar nu 8 med 4 för att få längden av kvadratens sida.
sidan=\frac{8}{4} sidan=2\;dmVi får att kvadratens sida har längden 2 dm.
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Vad är omkretsen av triangeln i bilden? Mät i figuren och svara i centimeter (cm).
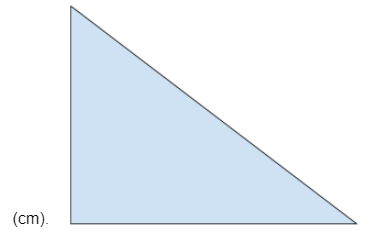
Svarsalternativ 1: 14 cm
Svarsalternativ 2: 16 cm
Svarsalternativ 3: 18 cm
Svarsalternativ 4: 24 cm
Korrekt svar: 24 cm
Fråga 2: Vad är omkretsen av rektangeln i bilden? Svara i meter (m).

Svarsalternativ 1: 10 m
Svarsalternativ 2: 20 m
Svarsalternativ 3: 24 m
Svarsalternativ 4: 40 m
Korrekt svar: 20 m
Fråga 3: En regelbunden femhörning har omkretsen 40 dm. Regelbunden betyder att varje sida i figuren är lika lång. Beräkna femhörningens sidlängd. Svara i decimeter (dm).
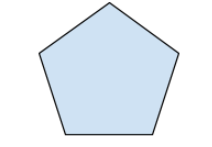
Svarsalternativ 1: 5 dm
Svarsalternativ 2: 6 dm
Svarsalternativ 3: 8 dm
Svarsalternativ 4: 12 dm
Korrekt svar: 8 dm
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

