Gränsvärde

Räkneexempel och förklaringar för gränsvärde:

Exempel 1: Hitta gränsvärdet \lim_{x \to 3} 2x +4

Svar: 10

Förklaring: Uppgiften frågar alltså vilket värde funktionen 2x+4 går mot då x närmar sig 3. En fiffig sak med gränsvärden är att om man kan stoppa in värdet direkt i funktionen så blir det alltid rätt. Om vi byter ut x mot tre i funktionen så får vi

2 \cdot 3 + 4  = 6 + 4 = 10

Gränsvärdet är därmed 10.

Exempel 2: Hitta gränsvärdet \lim_{x \to 0} \frac{3x}{x}

Svar: 3

Förklaring: Om vi försöker stoppa in värdet x=0 i funktionen så får vi:

\frac{3 \cdot 0}{0} = \frac{0}{0}

Det blir division med 0! Det betyder att vi inte kan stoppa in x direkt i funktionen eftersom funktionen inte är definierad i punkten x=0. Det vi istället får göra är att först förenkla funktionen. För att förenkla 

\frac{3 x}{x}

så kan vi se att både täljare och nämnare innehåller en faktor x. Alltså kan vi stryka x både över och under divisionstecknet:

\frac{3 \cdot x}{x} = \frac{3 \cdot \cancel{x}}{1 \cdot \cancel{x}} = 3

Så när x närmar sig noll,  så kommer funktionen vara konstant tre. Alltså är

\lim_{x \to 0} \frac{3x}{x} = 3

---

Exempel: Hitta funktionens gränsvärde \lim_{x \to 0} \frac{\sin x}{x} .

Svar: 1

Förklaring: Om vi försöker stoppa in x=0 i den här funktionen får vi igen division med noll. Det verkar heller inte gå att förenkla funktionen till någonting användbart. Låt oss istället undersöka funktionen för några olika värden på x. 

x	\frac{\sin x}{x}
1	0,8414709848
0.1	0,9983341665
0.01	0,9999833334
0.001	0,9999998333
0.0001	0,9999999983

Det verkar som att då x går närmre och närmre 0, så går \frac{\sin x}{x} närmre och närmre 1. Låt oss även studera  grafen till funktionen:

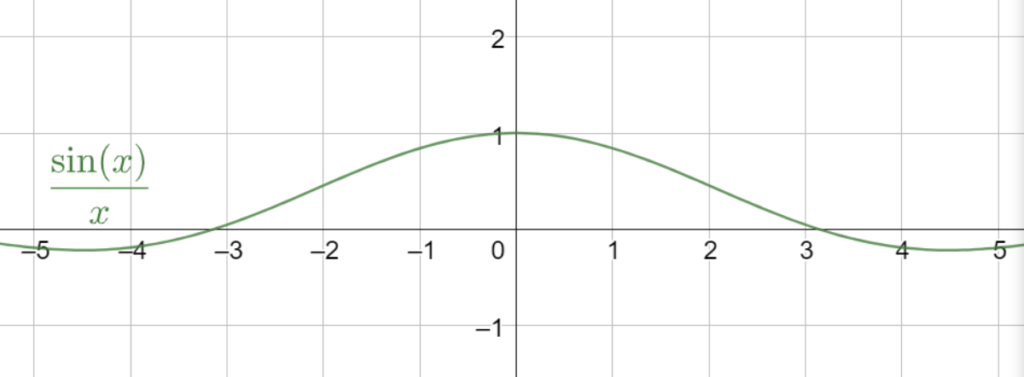
Där ser vi att vid x=0 så verkar grafen ha ett värde av 1. Men så är det inte! Funktionen är fortfarande odefinierad vid x=0, men det är nu ganska säkert att gränsvärdet är 1. Alltså:

\lim_{x \to 0} \frac{\sin x}{x} = 1

---

Exempel: Hitta funktionens gränsvärde \lim_{x \to 0} \frac{3}{x} .

Svar: Gränsvärdet existerar ej.

Förklaring: Om vi försöker stoppa in x=0 i funktionen så får vi division med 0. Genom att göra en tabell som i förra exemplet får vi 

x	\frac{3}{x}
1	3
0.1	30
0.01	300
0.001	3 000
0.0001	30 000

Funktionen bara stiger och stiger! Om vi även studerar grafen ser vi

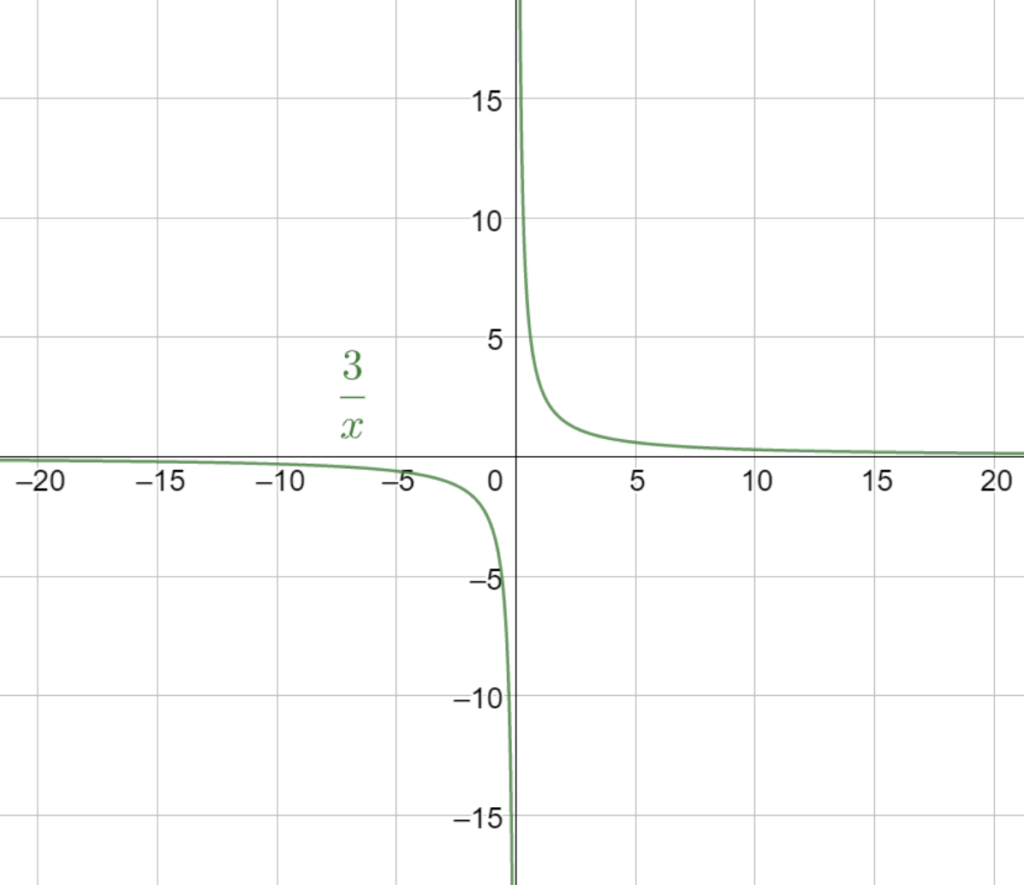
Funktionen går mot oändligheten! Formellt sett säger man då att gränsvärdet inte existerar. Man kan även säga att gränsvärdet är oändligt, men vi vill vara försiktiga! Om vi närmar oss 0 från positiva x så ser vi att grafen går mot positiva oändligheten.  Gränsvärdet blir då positiv oändlighet. Om vi istället går  mot noll från negativa X så går grafen neråt istället. Gränsvärdet blir negativ oändlighet. Det här kan skrivas som:

\lim_{x \to 0^{+}} \frac{3}{x} = \infty .

\lim_{x \to 0^{-}} \frac{3}{x} = -\infty .

Det här är lite fuskig notation, eftersom gränsvärdet inte existerar. Funktionen har alltså inga gränsvärden, men det är vanligt att skriva som ovan. När vi skriver 0^{+}   så menar vi att vi går mot noll från positiva x-värden.