Asymptoter
Asymptoter är räta linjer som en funktion närmar sig men aldrig korsar. Alla funktioner har inte asymptoter men för de som har dem kan de finnas i tre olika typer:
1. Horisontell asymptot, där funktionen långt bort från origo ser ut som en horisontell linje.
2. Vertikal asymptot, där funktionen långt bort från origo (i y-led) ser ut som en vertikal linje.
3. Sned asymptot, där funktionen långt bort från origo beter sig som en linje:
y = kx+m.
Låt oss kolla lite närmare på dessa tre typer!
Horisontell asymptot
Horisontell asymptot uppstår för en funktion som långt bort från origo ser ut som en horisontell linje. Med andra ord så har en funktion f(x) en horisontell asymptot om, då x blir större och större, så går f(x) mot ett konstant värde y=a. Alltså ska f(x) uppfylla:
\lim_{x \to +\infty} f(x) = aAlternativt
\lim_{x \to -\infty} f(x) = a .
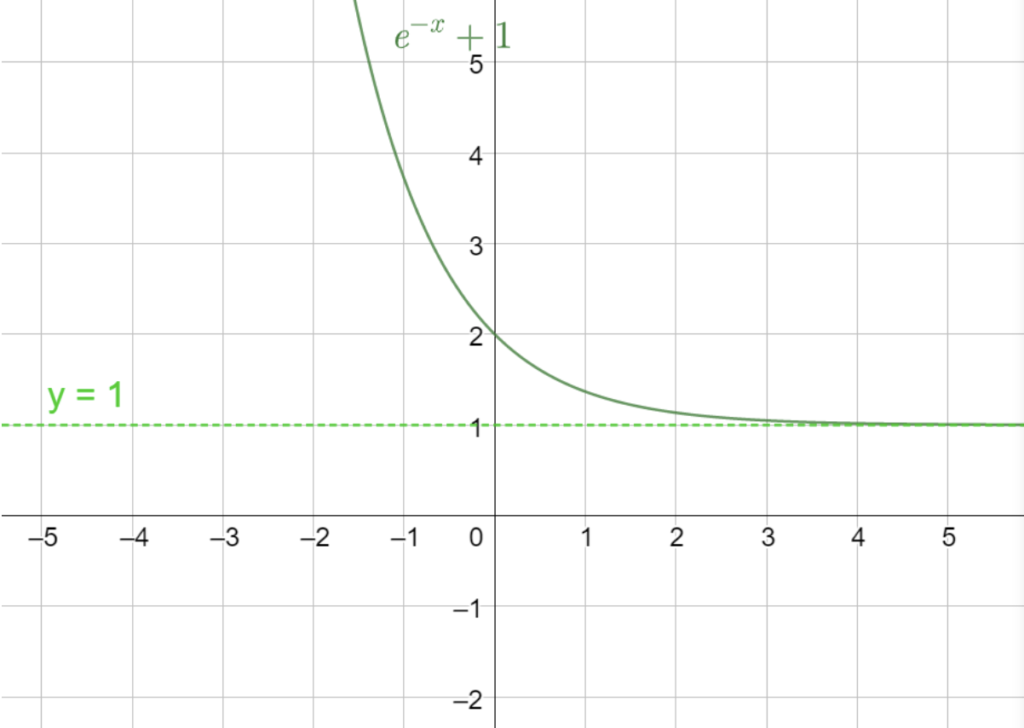
Vertikal asymptot
Vertikal asymptot uppstår för en funktion som långt bort från Origo (i y-led) ser ut som en vertikal linje. Med andra ord så har en funktion f(x) en vertikal asymptot om, då x närmar sig ett värde, så går f(x) mot oändligheten (positiv eller negativ). Alltså ska f(x) uppfylla:
\lim_{x \to a} f(x) = +\inftyalternativt
\lim_{x \to a} f(x) = -\infty
Sned asymptot
Sned asymptot uppstår hosen funktion som långt bort från origo ser ut som en linje y= kx + m. Alltså ska f(x) uppfylla:
då x går mot oändligheten. Mer rigoröst kan man subtrahera kx + m på båda sidor och ta gränsvärdet:
\lim_{x \to +\infty} f(x) - (kx+m) = 0alternativt
\lim_{x \to -\infty} f(x) - (kx+m) = 0
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

