Enhetscirkeln
Enhetscirkeln är en cirkel som har radie 1. En spännande egenskap hos enhetscirkeln är att den är ett jättebra redskap när man vill utforska trigonometriska förhållanden. Det här medför till exempel att när man vill räkna på cirkulär rörelse, såsom planeters omlopp, så kan man använda trigonometriska metoder! Enhetscirkeln är även väldigt användbar för att lista ut olika trigonometriska identiteter.
Vad är enhetscirkeln?
Enhetcirkeln har många användningsområden, särskilt inom trigonometri och koordinatsystem. Genom att använda enhetscirkeln kan man studera och analysera trigonometriska funktioner som sinus, cosinus och tangens och deras samband med vinklar. Genom att placera en vinkel i förhållande till enhetscirkeln kan man direkt avläsa sinus och cosinus för den givna vinkeln!
Varför är det då bra att förstå enhetscirkeln? Att kunna enhetscirkeln är bra eftersom den är grundläggande inom trigonometri, hjälper till att visualisera trigonometriska funktioner och underlättar beräkningar vid vanliga vinklar. Den visar funktionernas periodicitet och symmetri, vilket är viktigt för att lösa trigonometriska ekvationer. Dessutom används enhetscirkeln i fysik och ingenjörsvetenskap för att beskriva vågrörelser och roterande system. Den är också en grund för mer avancerad matematik, inklusive komplexa tal och calculus.
Räkneexempel och förklaringar för enhetscirkeln
Tanken med enhetscirkeln är att man i ett helt vanligt koordinatsystem ritar en cirkel med radie 1. Något som är ganska fiffigt är att för att specificera en punkt på enhetscirkeln så behöver vi bara säga hur långt man behöver rotera från x-axeln för att komma dit. I andra ord, en punkt på enhetscirkeln kan anges med bara en vinkel – i figuren ser vi att den gröna punkten på cirkeln har vinkeln 30° från x-axeln.
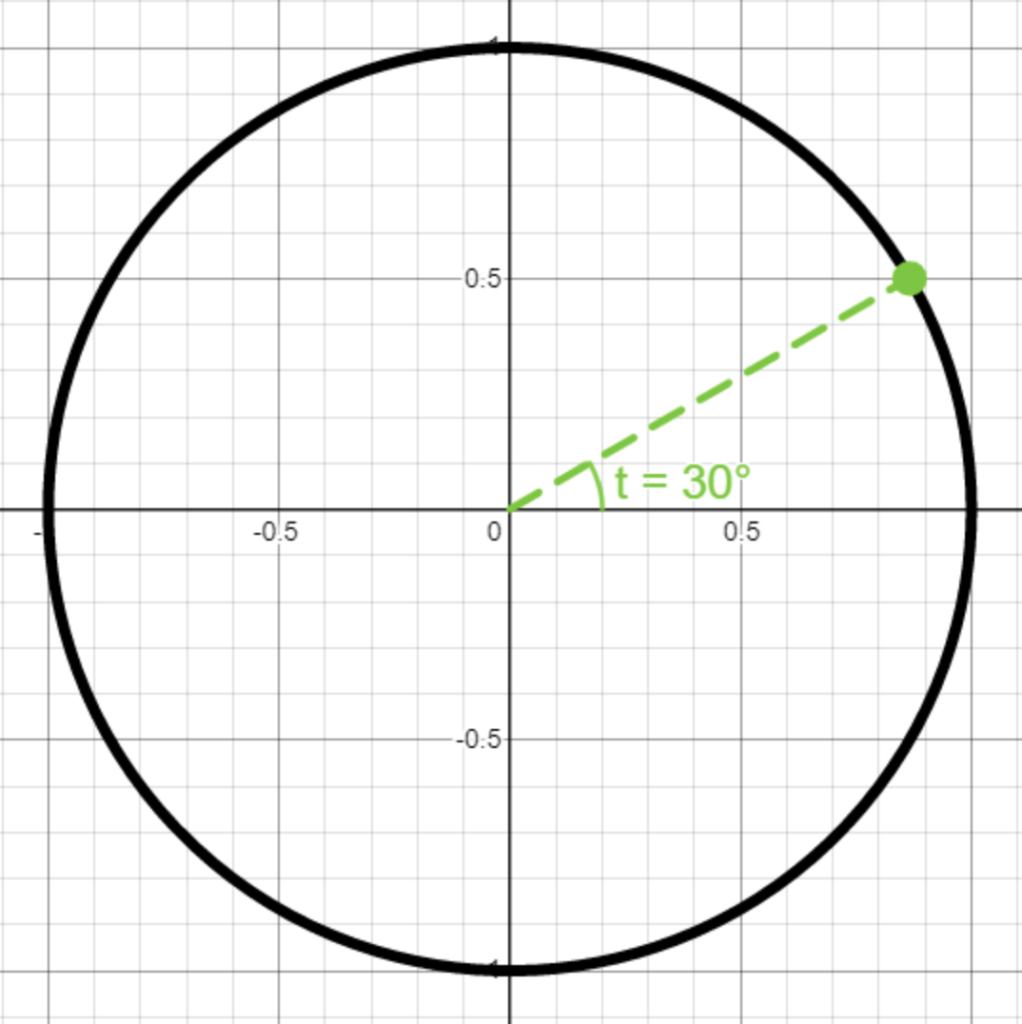
Men nu finns en spännande fråga, kan man konvertera från vinkeln till vanliga koordinater? Låt oss ta samma punkt – om vi vet att vinkeln är 30°, hur får vi fram x och y för punkten? Jo, koordinaten (x,y) betyder att man först går x steg åt höger, och sedan y steg uppåt. Om vi ritar in det i figuren får vi:
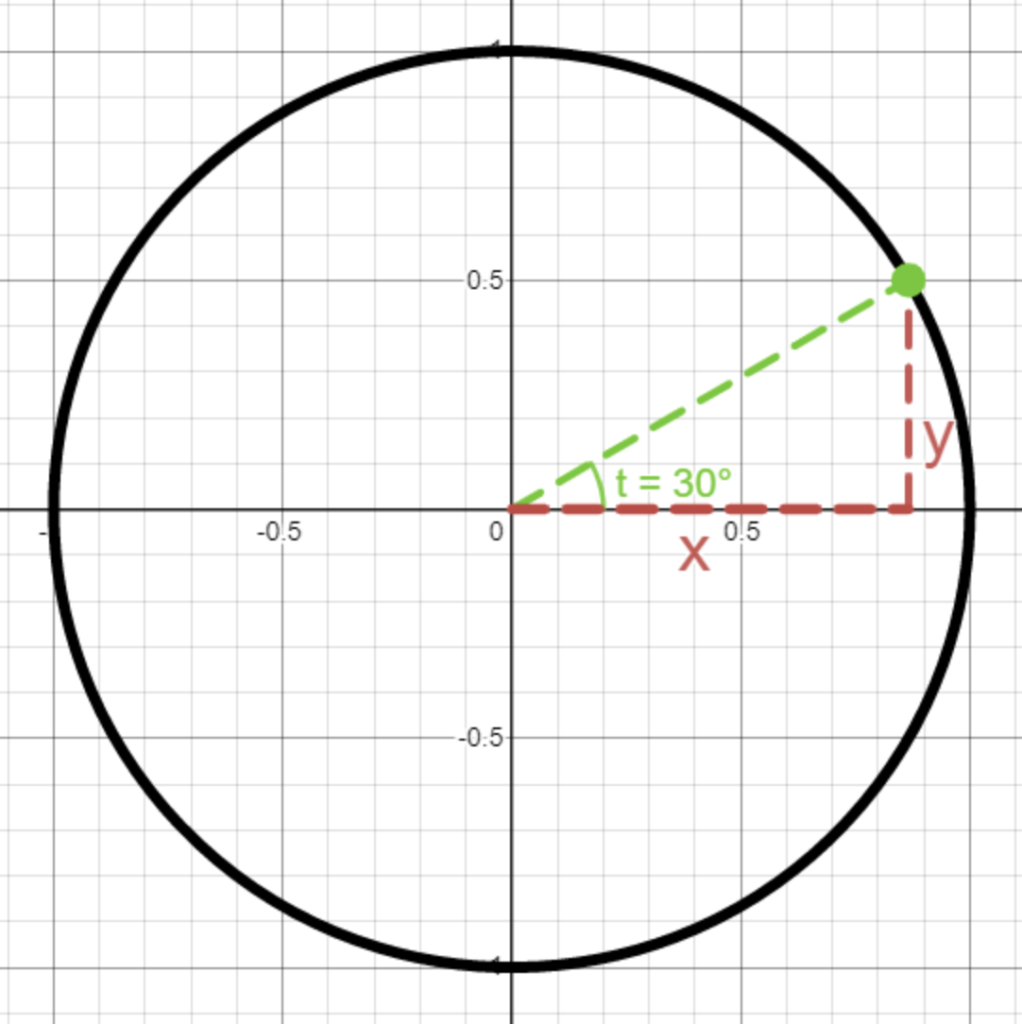
Men nu har något spännande hänt, vi har fått fram en rätvinklig triangel! Nu kan vi alltså använda trigonometri för att hitta förhållanden mellan vinkeln och koordinaterna x och y. I det här fallet har vi att den närliggande sidan till är x och att den motstående sidan är y. Men vad är hypotenusan? Från bilden kan vi se att hypotenusan är bara radien för cirkeln, men enhetscirkeln har ju radie 1! Vi får då relationerna \cos{30^{\circ}} = \frac{\text{n\"arliggande}}{\text{hypotenusa}} = \frac{x}{1} \sin{30^{\circ}} = \frac{\text{motst\aa ende}}{\text{hypotenusa}} = \frac{y}{1} och vi kan därmed hitta koordinaterna: x = \cos{30^{\circ}} = \frac{\sqrt{3}}{2} y = \sin{30^{\circ}} = \frac{1}{2} och koordinaterna för punkten är alltså \left( \frac{\sqrt{3}}{2} , \frac{1}{2} \right )
Förhållandena i enhetscirkeln
x = \cos{t} y = \sin{t} gäller inte bara för t = 30^{\circ}, utan för alla vinklar.
Exempel: Från figuren, vad är \cos{73^{\circ}}?

Från figuren har vi att för vinkeln 73° så är koordinaten på enhetscirkeln (0,29 ; 0,97). \cos{73^{\circ}} kommer motsvara x-koordinaten, vilken är 0,29.
Men vad händer om t är större än 90°? Det finns ju ingen rätvinklig triangel med en vinkel större än 90°, kan man ta sinus och cosinus då? Då är det så att man har bestämt att för enhetscirkeln ska alltid förhållandena x = \cos{t} , y = \sin{t} gälla, även för vinklar större än 90°.
Exempel: Från figuren, vad är \sin{140^{\circ}}?

Här är vinkeln större än 90°, så det finns ingen rätvinklig triangel som har den här vinkeln. Istället kan man använda enhetscirkeln för att hitta svaret! Från figuren har vi att enhetscirkeln vid vinkeln 140° har koordinaten (-0,77 ; 0,64). \sin{140^{\circ}} kommer då motsvara y-koordinaten för den här punkten, vilket är 0,64.
Enhetscirkeln kan även användas för att hitta olika trigonometriska identiteter.
Exempel: Vad är \cos{- 45^{\circ}}?
Vinkeln -45° betyder alltså att vi har roterat under x-axeln 45°.
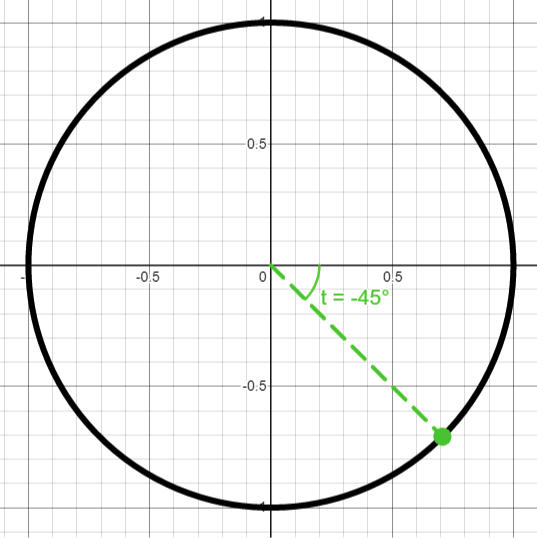
Vi söker cosinus, så vi vill använda x = \cos{t} . Vi söker alltså x-koordinaten för punkten. En smart sak man kan göra med enhetscirkeln är att även rita dit vinkeln 45, dvs den positiva motsvarigheten.

Nu ser vi att punkten med vinkeln -45 har samma x-koordinat som punkten med vinkeln 45 grader. Med x = \cos{t} har vi alltså att \cos{- 45^{\circ}} = \cos{45^{\circ}} nu kan vi slå upp cos 45 i en formelsamling, som säger \cos{45^{\circ}} = \frac{\sqrt{2}}{2} . Alltså har vi \cos{- 45^{\circ}} = \frac{\sqrt{2}}{2}
Mer generellt gäller, för alla vinklar t, att \cos{-t} = \cos{t} man kan med ett liknande argument få \sin{-t} = -\sin{t} .
På så liknande sätt kan fler identiteter tas fram!
Titta på genomgången
Få en riktig bra genomgång för att lära dig mer om enhetscirkeln. Med en video kan du pausa och gå tillbaka om det blir svårare att hänga med. Efter att ha sett genomgången är du väl rustad för att gå vidare med övningsuppgifterna nedan!
Övningsuppgifter för enhetscirkeln
Frågor med svarsalternativ:
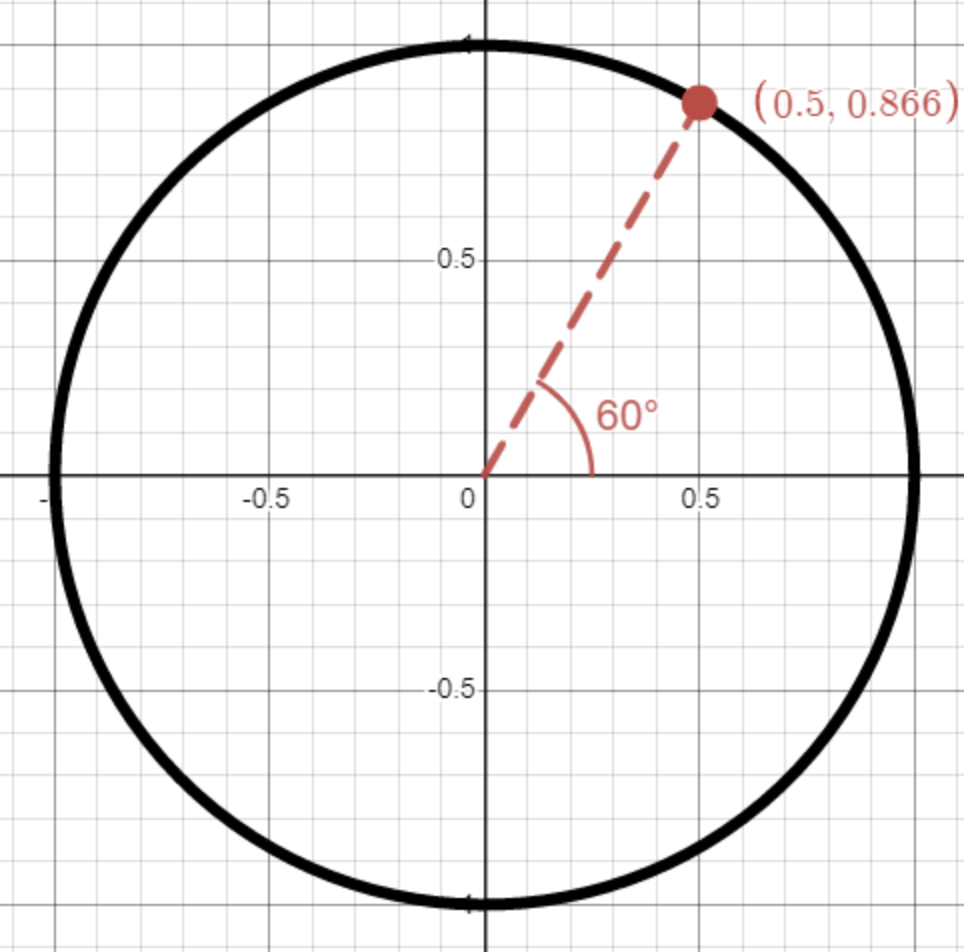
Fråga 1: Från bilden, vad är \cos{60^{\circ}}?
Svarsalternativ 1.1: 0,5 (rätt)
Svarsalternativ 1.2: 0,866
Svarsalternativ 1.3: -0,5
Svarsalternativ 1.4: -0,866
Fråga 2: Från bilden, vad är \sin{60^{\circ}}?
Svarsalternativ 2.1: 0,5
Svarsalternativ 2.2: 0,866 (rätt)
Svarsalternativ 2.3: -0,5
Svarsalternativ 2.4: -0,866
Fråga 3: Från bilden, vad är \sin{-60^{\circ}}?
Svarsalternativ 3.1: 0,5
Svarsalternativ 3.2: 0,866
Svarsalternativ 3.3: -0,5
Svarsalternativ 3.4: -0,866 (rätt)
Så hjälper Allakando dig till toppresultat i skolan

Mattehjälp för alla åldrar
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

