Lådagram
Lådagram är ett sätt att visualisera data och statistik, som både visar medianen för alla mätvärden, men också hur stor spridningen är. Detta uppnås genom att ta fram de så kallade kvartilerna! Målet är att beräkna en övre och en nedre kvartil så att 25% av mätvärdena ligger under den nedre kvartilen och 25% av mätvärdena ligger över den övre kvartilen. Från dessa kan man rita ett lådagram, som markerar det största och det minsta talet.
Hur ser ett lådagram ut?
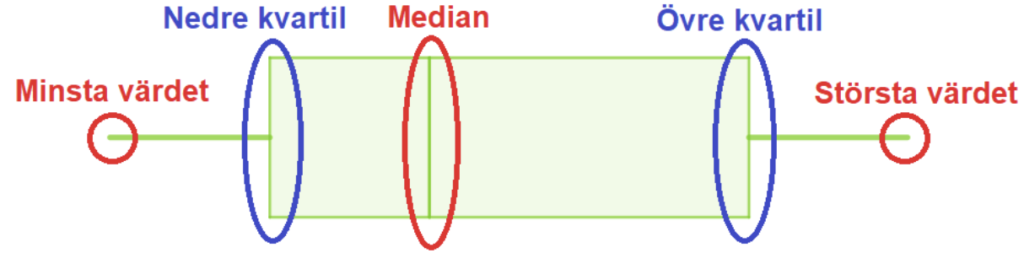
Ovan ser vi ett färdigritat lådagram. Genom ett lådagram får man en väldigt bra överblick över statistiken, eftersom lådagramet både visar runt var alla mätvärden ligger och även hur spridda de är.
Räkneexempel och förklaringar för lådagram:
Exempel 1: I bilden visas ett lådagram för längden av eleverna i en skolklass.
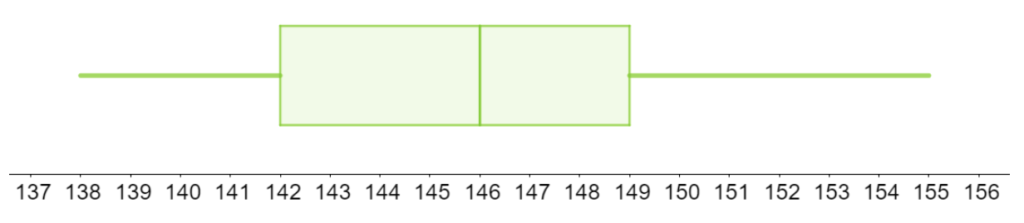
a) Hur lång är den längsta eleven i klassen?
Svar: 155 cm
Förklaring: De största och minsta värdena i lådagramet markeras i slutet av linjerna som sticker ut ur lådorna. I det här fallet så är det största värdet alltså 155 cm. Det är alltså längden för den längsta eleven.
b) Vad är medianen?
Svar: 146 cm
Förklaring: I mitten av lådagram 1 så har vi två lådor som möts. Stället där lådorna möts är medianen. I det här fallet har vi alltså medianen 146 centimeter.
c) Vad är den nedre kvartilen?
Svar: 142 cm
Förklaring: Nedre kvartil ligger vid änden av den vänstra lådan. I det här fallet så är det vid 142 cm. Alltså är nedre kvartil 142 cm.
Exempel 2: Vi har talserien 1, 2, 2, 4, 5, 7, 11, 12, 13, 15, 17
a) Hitta medianen
Svar: 7
Förklaring: Medianen är det mittersta talet. Eftersom vi i det här fallet har 11 tal, så kommer medianen vara det sjätte talet. Det sjätte talet är 7 , vilket då också är medianen. Talen måste vara i storleksordning!
b) Hitta den övre och den nedre kvartilen
Svar: 2 och 13.
Förklaring: Ett sätt för att räkna ut kvartiler är att man tar den övre eller nedre hälften av talen, och hittar medianen av dessa. Låt oss först kolla på den nedre kvartilen. Då tar vi alla tal som är mindre än medianen:
1, 2, 2, 4, 5Och så hittar vi medianen av dem. Vi har 5 tal, så medianen kommer vara det tredje talet. Alltså är medianen av de här fem talen 2. 2 är också därför den nedre kvartilen hos de ursprungliga 11 talen.
Härnäst gör vi samma sak för den övre kvartilen. Först tar vi fram alla tal som är större än medianen:
11, 12, 13, 15, 17Sedan hittar vi medianen för dem, som är 13. Den övre kvartilen är alltså 13.
c) Rita ett lådagram för talserien
Förklaring: Ett lådagram ritas vanligtvis över en tallinje. Låt oss därför först rita en tallinje.

De fem viktiga talen när man ritar ett lådagram är:
- Minsta talet
- Nedre kvartil
- Median
- Övre kvartil
- Största talet
Låt oss markera dessa fem över tallinjen:

Nu kan vi först rita lådorna i lådagramet. En låda från nedre kvartil till median och en låda från median till övre kvartil. Då ser det ut så här:
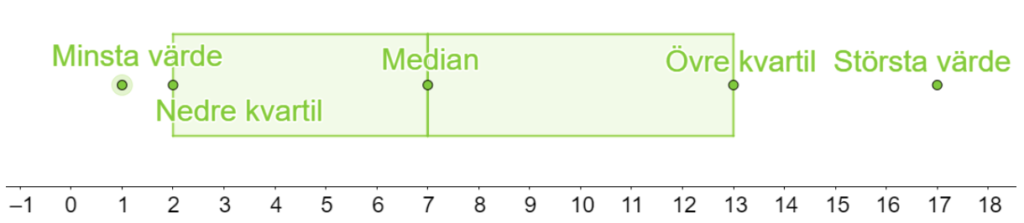
Till sist lägger vi till streck från lägre kvartil ner till minsta talet, och ett streck från övre kvartil till största talet. Så får vi att vårt lådagram ser ut som:
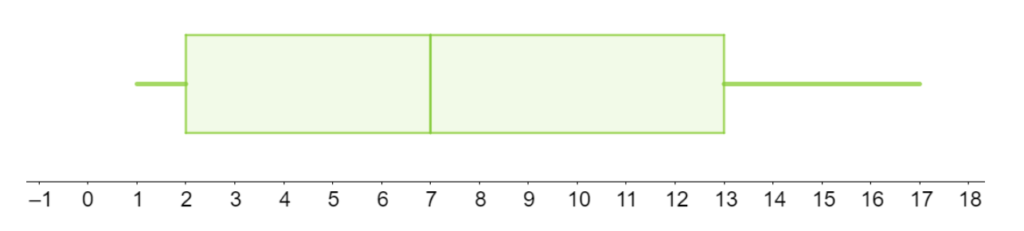
Övningsuppgifter
Frågor med svarsalternativ:
Rätt svar markeras i grönt.
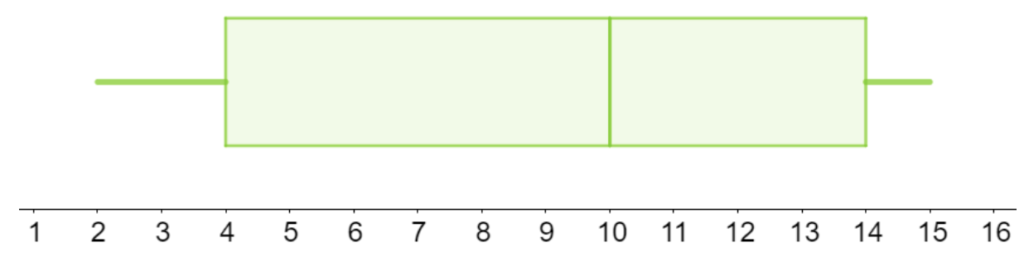
Fråga 1: Vad är medianen i lådagrammet ovan?
Svarsalternativ 1.1: 4
Svarsalternativ 1.2: 8
Svarsalternativ 1.3: 10
Svarsalternativ 1.4: 14
Fråga 2: Vad är minsta värdet i lådagrammet ovan?
Svarsalternativ 2.1: 1
Svarsalternativ 2.2: 2
Svarsalternativ 2.3: 3
Svarsalternativ 2.4: 4
Fråga 3: Vad är övre kvartil i lådagrammet ovan?
Svarsalternativ 3.1: 10
Svarsalternativ 3.2: 14
Svarsalternativ 3.3: 15
Svarsalternativ 3.4: 16
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

