Normalfördelning
När man undersöker ett fenomen så kan ens mätvärden vara fördelade på många olika sätt. En väldigt vanlig fördelning är den så kallade normalfördelningen. Normalfördelningar används inom väldigt många områden och beskriver till exempel hur djurs storlekar varierar eller hur temperaturen i en sjö varierar från dag till dag.
I den här guiden går vi igenom vad normalfördelning är och hur du kan använda dig av den inom matematiken. Längre ner hittar du exempeluppgifter med förklaringar samt övningar där du kan testa dina kunskaper!
Vad är normalfördelning?
En normalfördelning har egenskapen att de flesta av mätvärdena ligger kring medelvärdet, och ju längre ifrån medelvärdet man tittar desto färre mätvärden ser man. En annan viktig egenskap är att en normalfördelning är symmetrisk kring medelvärdet, det vill säga att det är lika många mätvärden över medelvärdet som under.
En viktig egenskap hos normalfördelningen är att den kan approximeras av en klockformad kurva, även kallad Gaussisk kurva eller klockkurva. Den är helt definierad av medelvärdet och standardavvikelsen och kurvan sträcker sig i båda riktningarna från medelvärdet.
Hur räknar man normalfördelning?
För att räkna på normalfördelningar bör man känna till standardavvikelsen. Standardavvikelsen är ett mått på hur mycket mätvärdena avviker i snitt från medelvärdet – om standardavvikelsen är hög så är mätvärdena väldigt spridda (men fortfarande koncentrerade kring medelvärdet).
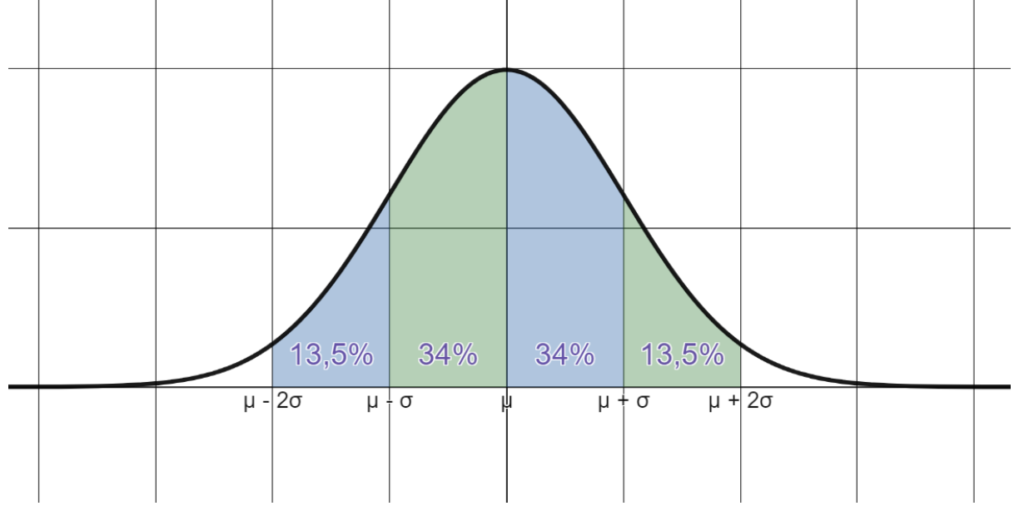
I bilden visas hur stor andel som täcks av varje omfång av standardavvikelse, där \mu betyder medelvärde och \sigma betyder standardavvikelse. Särskilt värt att notera är att
- 68% (34% + 34%) är mellan \mu - \sigma och \mu + \sigma , med andra ord så är 68% inom en standardavvikelse från medelvärdet.
- 95% (13,5% + 34% + 34% + 13,5%) är mellan \mu - 2 \sigma och \mu + 2 \sigma, med andra ord så är 95% inom två standardavvikelser från medelvärdet.
Exempel 1: På ett företag har man mätt att personalen har i genomsnitt längden 170 cm. Personalens längder är normalfördelad.
a) Om 95% av personalen är mellan 160 och 180 cm, vad är standardavvikelsen?
Svar: 5 cm
Förklaring: 160 cm och 180 cm är båda 10 cm från medelvärdet. Alltså är 95% av personalen inom 10 cm av medelvärdet. Eftersom att 95% är inom två standardavvikelser från medelvärdet när man har en normalfördelning, så är alltså 10 cm två standardavvikelser. Om två standardavvikelser är 10 cm så är en standardavvikelse 5 cm.
b) Hur stor andel av personalen är längre än 175 cm?
Svar: 16%
Förklaring: Låt oss först fastställa att 50% av personalen är längre än 170 cm, eftersom normalfördelningen är symmetrisk runt medelvärdet. Nu kan vi kolla på hur många standardavvikelser från medelvärdet 175 cm är. Eftersom standardavvikelsen är 5 cm så är 175 cm en standardavvikelse från medelvärdet. Uppgiften frågar alltså hur stor andel av personalen som är längre än en standardavvikelse från medelvärdet.
För att räkna ut det kan vi nu kolla på bilden som visar de olika andelarna för olika standardavvikelser. Därifrån ser vi nämligen att mellan \mu och \mu + \sigma är 34% av värdena. I det här fallet betyder det att 34% av personalen är mellan 170 cm och 175 cm långa. Så nu har vi att 50% är över 170 cm och att 34% är mellan 170 och 175 cm, vilket betyder att de över 175 cm är 50% - 34% = 16%!
Exempel 2: I en myrstack så kan vikten hos myrorna beskrivas med en normalfördelning.
De myror som är en standardavvikelse tyngre än medelvikten väger 8 gram, medan de som är två standardavvikelser tyngre än medelvikten väger 10 gram.
a) Vad är medelvikten för myrorna i myrstacken?
Svar: 6 gram
Förklaring: För att gå från en standardavvikelse över medelvärdet till två standardavvikelser över medelvärdet så ökar vi med exakt en standardavvikelse. I det här fallet går vi från 8 gram till 10 gram, vilket är en ökning på 2 gram. Alltså är en standardavvikelse 2 gram. Det betyder att 8 gram är 2 gram mer än medelvikten, vilket betyder att medelvikten är 6 gram.
Med \mu och \sigma kan ovanstående resonemang även skrivas:
\mu + \sigma = 8g och \mu + 2 \sigma = 10g
vilket betyder att (\mu + 2 \sigma) - (\mu + \sigma) = 10g - 8g
Vänstersidan kan förenklas enligt (\mu + 2 \sigma) - (\mu + \sigma) = \mu + 2 \sigma - \mu - \sigma = \sigma
Då vi får \sigma = 10g - 8g = 2g.
Vi kan nu stoppa in det i \mu + \sigma = 8g:
\mu + 2g = 8g och om vi tar minus 2g på båda sidor så får vi \mu = 6g .
b) Hur stor andel av myrorna har en vikt mellan 4 gram och 8 gram?
Svar: 68%
Förklaring: 4 gram är 2 gram under medelvärdet, och 8 gram är 2 gram över medelvärdet. Eftersom 2 gram är en standardavvikelse, så är frågan alltså om hur stor andel av myrorna som är inom en standardavvikelse av medelvikten. Enligt ovan så är det 68%!
Övningsuppgifter
Frågor med svarsalternativ:
Vid en undersökning på en skolklass hittar man att medellängden är 150 cm och 68% är mellan 146 cm och 154 cm.
Fråga 1: Vad är standardavvikelsen?
Svarsalternativ 1.1: 4 cm (rätt)
Svarsalternativ 1.2: 6 cm
Svarsalternativ 1.3: 8 cm
Svarsalternativ 1.4: 12 cm
Fråga 2: Hur stor andel är mellan 142 cm och 158 cm?
Svarsalternativ 2.1: 5%
Svarsalternativ 2.2: 34%
Svarsalternativ 2.3: 68%
Svarsalternativ 2.4: 95% (rätt)
Fråga 3: Hur stor andel är längre än 158 cm?
Svarsalternativ 3.1: 2,5% (rätt)
Svarsalternativ 3.2: 5%
Svarsalternativ 3.3: 34%
Svarsalternativ 3.4: 95%
Tips från Fredrik
Så lär du dig normalfördelning snabbt och enkelt

När det kommer till att lära sig räkna med normalfördelning är det viktigt att du har koll på grunderna. Normalfördelningen blir mycket lättare att förstå om du först känner dig säker på medelvärden och standardavvikelser.
Det är också viktigt att förstå att normalfördelningen i grunden är en teoretisk modell. När det kommer till verkliga mätningar, är det vanligt att de uppvisar en fördelning som påminner om en klockkurva, men det är ovanligt att den är exakt identisk. Det är ofta beskrivet som att mätvärdena följer en approximativ normalfördelning.
Om du tycker att det känns knepigt med normalfördelning – oroa dig inte! På Allakando har vi många erfarna studiecoacher som har bemästrat statistiken och gärna hjälper dig. Med rätt vägledning och lite övning kommer normalfördelningen bli lättare på nolltid!

Fredrik Fridlund, VD & Grundare
Har själv undervisat över 3 000 elever sedan 2007
Så hjälper Allakando dig till toppresultat i skolan

Mattehjälp för alla åldrar
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

