Radie och diameter
Alla cirklar har en radie och en diameter. Radien och diametern är två olika avstånd och de används för att beskriva cirkelns storlek.
Det är viktigt att förstå skillnaden mellan radie och diameter när man arbetar med cirkulära figurer och cirkelrelaterade beräkningar. Båda termer används för att beskriva olika aspekter av en cirkel och de är sammankopplade genom en enkel matematisk relation.
Vad är radie?
Radien är avståndet från cirkelns medelpunkt till dess kant. Den är alltid en rak linje. Vi betecknar den med ett r. Radien kommer alltid vara lika stor oavsett vilken punkt på cirkelns kant vi väljer att dra den till. Det kan också tänkas som halva diameter.
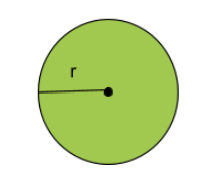
Vad är diameter?
Diametern är avståndet mellan två motsatta punkter på cirkelns kant. Diametern är en rak linje och den måste alltid gå genom medelpunkten. Vi betecknar den med ett d. Precis som med radien så kommer diametern alltid vara lika stor, förutsatt att den är en rak linje som går från kant till kant, genom medelpunkten.
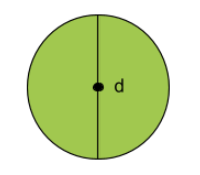
Diametern är relaterad till radien eftersom diametern är dubbelt så lång som radien. Detta förhållande kan illustreras i ekvationen: d = 2r (d är diameter och r är radien).
Diameter kan även användas för att beräkna cirkelns omkrets genom formeln C=π, där C är omkretsen och π är pi, en matematisk konstant (ungefär 3.143.14).
Här hittar du vår guide för hur man räknar ut cirkelns omkrets och area
Därför är det bra att kunna räkna med radie och diameter
Att förstå radie och diameter är viktigt av flera anledningar. Dessa begrepp är grundläggande inom geometri och används för att definiera och beräkna egenskaper hos cirklar och sfärer, såsom omkrets, area, volym och yta. Kunskapen är också praktiskt användbar inom områden som bygg och ingenjörskonst, där man ofta arbetar med runda föremål som hjul och rör. Dessutom hjälper förståelsen av radie och diameter till att lösa matematiska problem, utveckla logiskt tänkande och förbereda för avancerade studier inom matematik och vetenskap, inklusive fysik och trigonometri.
Räkneexempel av radie och diameter
Nedan ser vi en cirkel där både radien och diametern är utmarkerade.
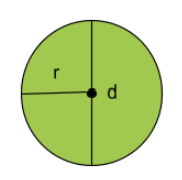
Vi upptäcker när vi kollar på figuren att vi kan dela upp diametern i två delar. Den första delen är den linje som går ovan medelpunkten och den andra delen är den linje som går under medelpunkten.
De två delarna av diametern kommer båda ha måtten \frac{d}{2}.
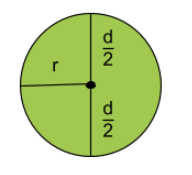
Nu ser vi att diametern delat på två faktiskt är avståndet mellan cirkelns medelpunkt och dess kant, vilket är samma sträcka som radien!
Detta innebär att \frac{d}{2}=r.
Vi kan multiplicera båda sidorna av uttrycket med 2.
\frac{d}{2}=r {2}\cdot{\frac{d}{2}}={2}\cdot{r} d={2}\cdot{r}Vi får att d={2}\cdot{r}, vilket betyder att diametern är dubbelt så stor som radien.
Exempel 1: Figuren i bild är en cirkel. Vilken av de två sträckorna, a och b, är cirkelns radie respektive diameter?
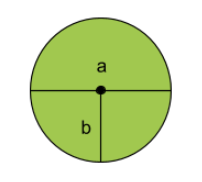
Svar: Sträckan b är cirkelns radie. Sträckan a är cirkelns diameter.
Lösning: Vi ser att sträckan a är en rak linje mellan två motsatta punkter på cirkelns kant. a passerar även genom cirkelns medelpunkt. Därmed vet vi att sträckan a är cirkelns diameter.
Vidare ser vi att sträckan b är en rak linje från cirkelns medelpunkt till dess kant. Det innebär att b är cirkelns radie.
Exempel 2: En cirkel har diametern 8 centimeter. Bestäm cirkelns radie.
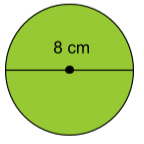
Svar: 4\;cm
Lösning: Cirkelns diameter är 8 centimeter lång. Vi vet sedan innan att cirkelns diameter är dubbelt så stor som dess radie. Sambandet d={2}\cdot{r} visar detta förhållande. d är cirkelns diameter och r är dess radie.
Vi börjar med att sätta in att d=8\;cm i sambandet d={2}\cdot{r}.
8={2}\cdot{r}Vi vill att radien, r, ska stå ensamt till höger om likamedtecknet. Därför delar vi båda sidor med 2, vilket gör så att tvåan bredvid radien, r, flyttas över.
\frac{8}{2}=\frac{{2}\cdot{r}}{2} \frac{8}{2}=rVi behöver nu endast förenkla vänster led, genom att beräkna \frac{8}{2}.
\frac{8}{2}=r r=4\;cmVi får att radien är 4 centimeter.
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Figuren i bild är en cirkel. Vilken av de två sträckorna, x och y, är cirkelns radie respektive diameter?
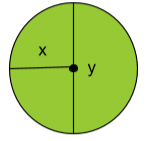
Svarsalternativ 1.1: Sträckan x är cirkelns radie. Sträckan y är cirkelns diameter.
Svarsalternativ 1.2: Sträckan y är cirkelns radie. Sträckan x är cirkelns diameter.
Svarsalternativ 1.3: Både x och y är diametrar
Svarsalternativ 1.4: Både x och y är radier
Korrekt svar: Sträckan x är cirkelns radie. Sträckan y är cirkelns diameter.
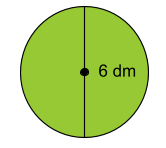
Fråga 2: En cirkel har diametern 6 decimeter. Bestäm cirkelns radie.
Svarsalternativ 2.1: 2\;dm
Svarsalternativ 2.2: 3\;dm
Svarsalternativ 2.3: 4\;dm
Svarsalternativ 2.4: 5\;dm
Korrekt svar: 3\;dm
Fråga 3: En cirkel har radien 11 centimeter. Bestäm cirkelns diameter.
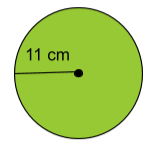
Svarsalternativ 3.1: 5,5\;cm
Svarsalternativ 3.2: 6\;cm
Svarsalternativ 3.3: 11\;cm
Svarsalternativ 3.4: 22\;cm
Korrekt svar: 22\;cm
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

