Rätblockets volym
Ett rätblock är en figur där alla sidor består av rektanglar. Dess form påminner om en tegelsten eller ett mjölkpaket.
Detta är ett rätblock
Ett rätblock är en tredimensionell geometrisk figur som har sex sidor, varav varje sida är en rektangel. I ett rätblock möts alla hörn vinkelrätt, vilket innebär att alla vinklar är räta, det vill säga 90 grader. Rätblocket är ett specialfall av en prisma, där basytan är en rektangel.
Rätblocket har följande egenskaper:
- Sex sidor (ytter) som alla är rektanglar.
- Tre par av motsatta sidor som är kongruenta (exakt lika i form och storlek).
- Tolv kanter, där varje par av motstående kanter är lika långa.
- Åtta hörn där tre kanter möts i varje hörn.
Ett rätblock har tre olika mått: en längd (l), en bredd (b), och en höjd (h).
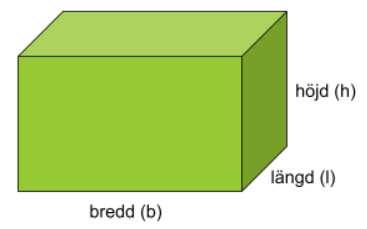
Dessa mått lägger grunden för rätblockets volym. Vi beräknar rätblockets volym med sambandet Volym={basytan}\cdot{höjd}.
Eftersom basen har formen av en rektangel vet vi att basytan={längd}\ct{bredd}.
Vi kan därför skriva om volymen genom att ersätta basytan med uttrycket {längd}\cdot{bredd}. Vi får då att Volym={längd}\cdot{bredd}\cdot{höjd}.
Vi kan även skriva att Volym={l}\cdot{b}\cdot{h}.
Så räknar du ut rätblockets volym
Exempel 1: Beräkna rätblockets volym. Svara i cm^3.
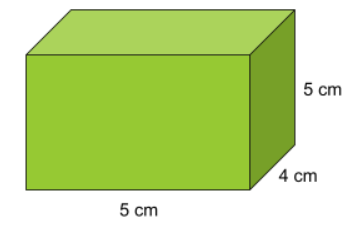
Svar: 100\;cm^3
Lösning: Vi använder sambandet Volym={längd}\cdot{bredd}\cdot{höjd} för att beräkna rätblockets volym.
- Vi börjar med att identifiera längden, bredden och höjden av rätblocket. Vi ser att:
2. Vi sätter nu in dessa värden i sambandet Volym={längd}\cdot{bredd}\cdot{höjd}.
Volym={längd}\cdot{bredd}\cdot{höjd}= {5}\cdot{4}\cdot{5}3. Vi börjar med att multiplicera de två vänstra faktorerna.
{5}\cdot{4}\cdot{5}=
{20}\cdot{5}
4. Nu behöver vi endast multiplicera de två återstående talen.
Volym={20}\cdot{5}= 100\;cm^3Vi får att rätblockets volym är 100\;cm^3
Exempel 2: Beräkna rätblockets volym. Svara i liter.
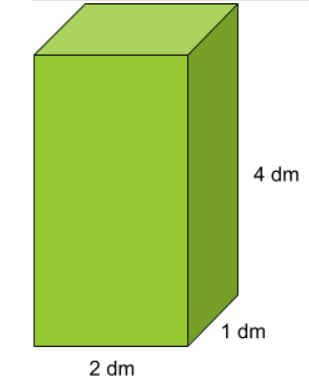
Svar: 8\;liter
Lösning: Vi använder även här sambandet Volym={längd}\cdot{bredd}\cdot{höjd} för att beräkna rätblockets volym.
- Vi börjar med att identifiera rätblockets mått.
Vi sätter nu in dessa värden i sambandet Volym={längd}\cdot{bredd}\cdot{höjd}.
Volym={längd}\cdot{bredd}\cdot{höjd}= {2}\cdot{1}\cdot{4}Vi multiplicerar de två vänstra faktorerna.
{2}\cdot{1}\cdot{4}=
{2}\cdot{4}
Sedan multiplicerar vi talen som är kvar.
{2}\cdot{4}= 8\;dm^3Nu vill vi omvandla volymen från dm^3 till liter.
Vi kommer ihåg att 1\;liter=1\;dm^3[latex]. Liter och [latex]dm^3 har alltså samma mått. Därmed vet vi att 8\;dm^3=8\;liter.
Vi får att rätblockets volym är 8\;liter
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Beräkna rätblockets volym. Svara i m^3.
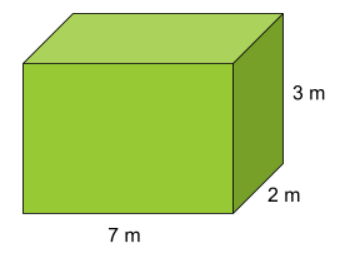
Svarsalternativ 1.1: 28\;m^3
Svarsalternativ 1.2: 32\;m^3
Svarsalternativ 1.3: 36\;m^3
Svarsalternativ 1.4: 42\;m^3
Korrekt svar: 42\;m^3
Fråga 2: Beräkna rätblockets volym. Svara i cm^3.
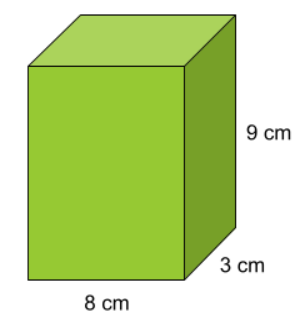
'Svarsalternativ 2.1: 104\;cm^3
Svarsalternativ 2.2: 208\;cm^3
Svarsalternativ 2.3: 216\;cm^3
Svarsalternativ 2.4: 316\;cm^3
Korrekt svar: 216\;cm^3
Fråga 3: Beräkna rätblockets volym. Svara i dl. Avrunda till två decimaler.
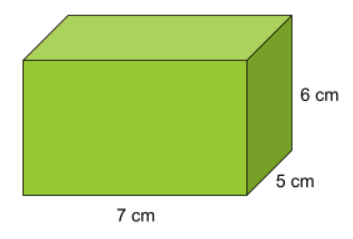
Svarsalternativ 3.1: 1,80\;dl
Svarsalternativ 3.2: 1,85\;dl
Svarsalternativ 3.3: 1,95\;dl
Svarsalternativ 3.4: 2,10\;dl
Korrekt svar: 2,10\;dl
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

