Vinklar
I alla geometriska former med räta linjer hittar vi vinklar. Vidgar vi vyerna och tänker på vinklar i vardagen upptäcker vi snabbt att de finns i princip överallt. De förekommer i husens konstruktion, skidbackens lutning, till och med i den skärm du använder för att läsa den här guiden. Eftersom att vinklar är en så vanlig och viktig aspekt i vår värld, är det viktigt att ha en grundläggande förståelse för dem.
I den här guiden har vi samlat förklaringar för de olika typerna av vinklar och uppgifter så att du kan lära dig räkna med dem snabbt och enkelt!
Vad är en vinkel?
När två linjer möts så kan vi prata om vinkeln på dem. Vinkeln beskriver hur stort gapet mellan de två linjerna är. Går linjerna väldigt tätt intill varandra bildar de en liten vinkel och om de går åt väldigt olika håll så bildar de istället en stor vinkel. De två linjerna som möts kallar vi för vinkelns ben och punkten där de möts kallar vi för vinkelns spets.
Vi kan också tänka på vinklar som en rotation! Om du står vänd och kollar längs med ena vinkelbenet och roterar tills att du står i det andra vinkelbenets riktning, så mäter vinkeln hur mycket du har roterat.
För att mäta vinklar använder vi en enhet som kallas för grader och ser ut så här °. Om du roterar ett helt varv, alltså tills du står i samma riktning som du började med, så har du roterat 360 grader. Mindre vinklar hittar vi genom att dela 360: Ett halvt varv är därför 180 grader, och ett fjärdedels varv är 90 grader.
Olika typer av vinklar
Rät vinkel
En rät vinkel är alltid exakt 90 grader, alltså ett fjärdedels varv. Ibland kan det vara lite svårt att se om vinkeln är precis 90 grader och därför använder vi oss av en liten kvadrat vid vinkelns spets för att markera att vinkeln är rät. Ser du den kan du vara säker på att vinkeln är exakt 90 grader.
Trubbig vinkel
Om en vinkel är större än 90 grader men mindre än 180 grader kallar vi den för en trubbig vinkel. Alltså är värdet på vinkeln 90° < v < 180°.
Spetsig vinkel
Vinklar som är mindre än 90 grader kallas för spetsiga vinklar. Värdet för dessa vinklar är alltså 0° < v < 90°.
Rak vinkel
En rak vinkel är exakt 180 grader och ser alltså ut som en rak linje.
Här kan du läsa mer om trubbig och spetsig vinkel!
Räkneexempel och förklaringar för vinklar:
Exempel 1: Ordna följande vinklar från minst till störst:
Svar: A, C, B
Förklaring:
Man kan tänka vinkeln som hur stort gapet är mellan vinkelbenen. I det här fallet är vinkel A den med minst gap mellan vinkelbenen, så den har också minst vinkel. Vinkel B har mycket större gap än vinkel C, så den har störst vinkel. Alltså har de ordningen A, C, B.
För att visualisera en vinkel så brukar man rita en båge mellan vinkelbenen, detta kallar vi för vinkelbåge. I det här fallet ser det då ut så här:
För att jämföra vinklars storlek så kan man då jämföra hur stor bågen är för vinklarna. I det här fallet så har vinkel A minst båge, vinkel B har störst båge, och vinkel C är mitt emellan. Alltså är vinklarna i storleksordning A, C, B.
Exempel 2: Ordna följande vinklar från minst till störst:
Svar: B, A, C
Förklaring: Låt oss markera vinklarna med bågar:
Nu är det lite lättare att se vinklarnas storlek. Den vinkel som har minst båge är vinkel B. Vinkel B är alltså den minsta vinkeln. Mellan A och C så har vinkel C en större båge än vinkel A. Alltså är vinkel C den största vinkeln. Vinklarna i storleksordning är då B, A, C.
Exempel 3: Vinklarna i figuren är 30 grader, 70 grader, och 140 grader. Identifiera vilken vinkel som är vilken.
Svar: A = 70 grader, B = 140 grader, C = 30 grader
Förklaring: Det minsta talet som är angivet är 30 grader. Alltså måste den minsta vinkeln vara 30 grader. Jämför vi vinkelbågarnas storlek så ser vi att vinkel C är minst. Vinkel C måste därför vara 30 grader. Vi har då kvar 70 och 140 grader och 140 det största alternativet. Den största vinkeln i figuren är vinkel B. Alltså är vinkel B 140 grader. Kvar har vi vinkel A som då måste vara 70 grader.
Övningsuppgifter
Frågor med svarsalternativ:
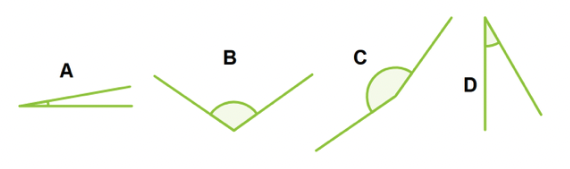
Rätt svar markeras i grönt.
Fråga 1: Vilken av vinklarna är minst?
Svarsalternativ 1.1: A
Svarsalternativ 1.2: B
Svarsalternativ 1.3: C
Svarsalternativ 1.4: D
Fråga 2: Vilken av vinklarna är störst?
Svarsalternativ 2.1: A
Svarsalternativ 2.2: B
Svarsalternativ 2.3: C
Svarsalternativ 2.4: D
Fråga 3: Vinklarnas mått är 10°, 30°, 110° och 160°. Vilken vinkel är 110°?
Svarsalternativ 3.1: A
Svarsalternativ 3.2: B
Svarsalternativ 3.3: C
Svarsalternativ 3.4: D
Fredrik tipsar
Så räknar du ut vinkelns storlek

För att ta reda på hur stor en vinkel är kan vi använda oss av en gradskiva. En gradskiva är ett mätverktyg som ser ut ungefär som en cirkelformad linjal och placeras längs utmed ena vinkelbenet. Om du inte har en gradskiva kan du ibland ta hjälp av olika geometriska egenskaper och samband mellan närliggande vinklar för att räkna ut storleken!
Ett exempel på en situation då detta är möjligt är när två räta linjer korsar varandra och bildar ett X med fyra vinklar. Vi kan då räkna ut storleken på alla vinklar så länge vi vet hur stor en av dem är! Detta beror på att vinklar som ligger mittemot varandra, även kallade vertikalvinklar, alltid är lika stora. Om du vet att en vinkel mäter 45°, måste alltså dess motsatta vinkel också vara 45°. Detta gäller även för de återstående vinklarna. Eftersom att de ligger mitt emot varandra måste de vara 135 grader vardera för att totalt uppgå till 360 grader, vilket är ett helt varv.
Känns vinklar eller någon annan del av matten krånglig? Oroa dig inte, på Allakando har vi massvis med mattecoacher som har blivit experter på geometri och är riktigt bra på att förklara!

Fredrik Fridlund, VD & Grundare
Har själv undervisat över 3 000 elever sedan 2007
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

