Volym och volymenheter
Det finns flera sätt att mäta geometriska figurer. Du har förmodligen redan bekantat dig med att beräkna omkretsen och arean av olika figurer, men det finns också en annan viktig aspekt att mäta – nämligen volymen av en figur.
Denna guide kommer att presentera olika förklaringar av vad volym innebär, vilka enheter vi använder för att mäta volym, samt ge exempel på hur de tillämpas. Längst ner på sidan hittar du övningsuppgifter att träna på att beräkna volym!
Vad är volym?
Volym är den mängd som ett föremål rymmer. Beroende på föremålets form använder vi oss av olika metoder för att beräkna dess volym.
För många av de enklare figurerna gäller dock att vi kan beräkna volymen med hjälp av sambandet Volymen={basytan}\cdot{höjden}. Detta gäller för bland annat kuber, rätblock och cylindrar.
Hur mäter vi volym?
Det finns två olika sorters enheter för volym som vi kommer lära oss om i detta avsnitt. Den ena typen av enheter är literenheter. Där inkluderas liter, deciliter, centiliter och milliliter. Literenheterna förkortas till l, dl, cl och ml. Ofta använder vi dock inte förkortningen för just liter eftersom den lätt kan misstas för en etta.
Den andra typen av enheter är de enheter som börjar med frasen “kubik”. Där ingår bland annat kubikmeter, kubikdecimeter och kubikcentimeter. Dessa enheter skrivs som m^3, dm^3 och cm^3. Enheten kubikmillimeter (mm^3) finns även, men används sällan.
Så omvandlar du volymenheter
Det mest vardagliga måttet för volym är litern. Volymen 1 liter är ungefär storleken av ett vanligt mjölkpaket. Det finns även deciliter (dl), centiliter (cl) och milliliter (ml). Måtten förhåller sig enligt nedan.
1\;liter=10\;dl 1\;dl=10\;cl 1\;cl=10\;mlSammanfattningsvis gäller att 1\;liter=10\;dl=100\;cl=1\;000\;ml.
Exempel 1: Omvandla 320 centiliter till liter
Svar: 3,2\;liter
Lösning: Vi ser ovan att 100\;cl=1\;liter.
Vi delar båda sidorna med 100 och får att 1\;cl=0,01\;liter.
Vi kan därmed ersätta cl med 0,01\;liter i uttrycket 320 cl.
320\;cl={320}\cdot{0,01\;liter}=3,2\;liter
Vi får att 320 cl är lika med 3,2\;liter
Enheterna kubikmeter (m^3), kubikdecimeter (dm^3) och kubikcentimeter (cm^3) förhåller sig lite annorlunda än literenheterna. Här gäller att:
1\;m^3=1\;000\;dm^3 1\;dm^3=1\;000\;cm^3Man kan alltså skriva att 1\;m^3=1\;000\;dm^3=1\;000\;000\;cm^3
Det noterbara är alltså att man multiplicerar eller delar med 1\;000 för att omvandla till nästa enhet.
Vi kan visa varför detta gäller genom att ta ett exempel med en kub där alla sidor har måttet 1 meter. En kub är en figur där sidorna är kvadrater och alla sidor är lika långa.
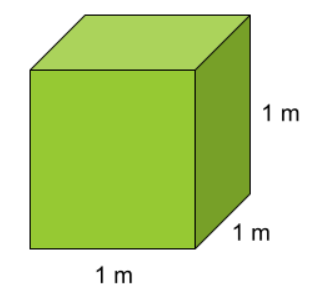
Vi beräknar kubens volym med sambandet Volymen={basytan}\cdot{höjden}.
Vi börjar med att beräkna basytan. Basen har formen av en kvadrat. Vi räknar därför ut basytan med sambandet basytan={sidan}\cdot{sidan}. Vi ser i figuren att sidan har måttet 1 meter.
basytan={sidan}\cdot{sidan}={1\;m}\cdot{1\;m}=1\;m^2
Basytan är 1\;m^2 stor.
Vi sätter in detta i sambandet Volymen={basytan}\cdot{höjden} och ser att Volymen={1\;m^2}\cdot{höjden}.
Höjden är 1 meter.
Volymen={1\;m^2}\cdot{höjden}= {1\;m^2}\cdot{1\;m}= 1\;m^3Vi får att volymen av kuben är 1\;m^3.
Samtidigt vet vi att 1\;m=10\;dm. Vi kan därmed även rita exakt samma kub så här:
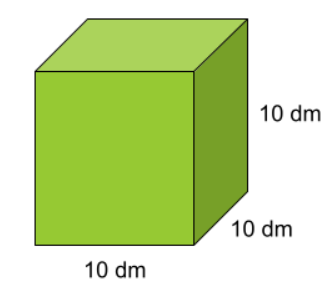
Vi räknar ut volymen på samma sätt som innan, fast med sidan som 10 dm.
Volymen={basytan}\cdot{höjden} Basytan={sidan}\cdot{sidan}= {10\;dm}\cdot{10\;dm}= 100\;dm^2 Volymen={100\;dm^2}\cdot{höjden}= {100\;dm^2}\cdot{10\;dm}= 1\;000\;dm^3Vi får att volymen av kuben är 1\;000\;dm^3.
Samma kub har alltså både volymen 1\;m^3 och 1\;000\;dm^3.
Detta betyder att 1\;m^3=1\;000\;dm^3, vilket gäller för alla figurer där vi räknar med samma enheter, inte bara kuber.
Exempel 2: Beräkna kubens volym. Svara i dm^3. Avrunda till en decimal
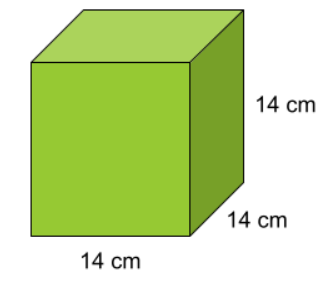
Svar: 2,7\;dm^3
Lösning: Vi börjar med att omvandla kubens sidor från centimeter till decimeter. Vi vet att 10\;cm=1\;dm, därmed gäller att 14\;cm=1,4\;dm. Vi skriver om enheterna så att de är skrivna i decimeter.
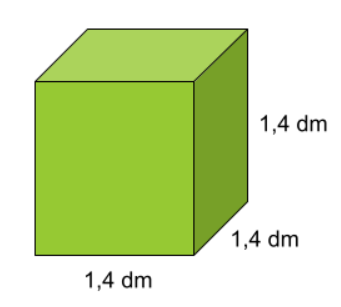
Nu börjar vi att räkna ut kubens volym med hjälp av sambandet Volymen={basytan}\cdot{höjden}.
Eftersom kuben har en kvadratisk bas gäller att basytan={sidan}\cdot{sidan}.
Sidan är 1,4\;dm.
basytan={sidan}\cdot{sidan}= {1,4}\cdot{1,4}= 1,96\;m^2 Volymen={basytan}\cdot{höjden}= {1,96}\cdot{höjden}Höjden är 1,4\;dm.
Volymen={1,96}\cdot{höjden}= {1,96}\cdot{1,4}= 2,744\;dm^3Vi får att kubens volym är 2,744\;dm^3. Avrundat till en decimal blir detta 2,7\;dm^3.
Vi kan även omvandla mellan literenheterna och kubikenheterna. Det är nämligen så att en liter faktiskt är exakt samma sak som en dm^3.
1\;liter=1\;dm^3Med detta följer även att en milliliter är samma sak som en cm^3.
1\;ml=1\;cm^3Dessa två samband är mycket användbara när vi omvandlar från literenheter till kubikenheter.
Exempel 3: Omvandla 2 deciliter till cm^3
Svar: 200\;cm^3
Lösning: Vi vill omvandla 2 deciliter till cm^3. Eftersom vi vet att 1\;ml=1\;cm^3 kan vi därmed börja med att omvandla 2 deciliter till milliliter.
Vi vet att 1\;dl=100\;ml. Därför kan vi ersätta dl med 100\;ml i uttrycket 2 dl.
2\;dl= {2}\cdot{100\;ml}=200\;ml
2 dl är alltså detsamma som 200\;ml.
Nu behöver vi endast omvandla 200 milliliter till cm^3. Vi ser då att 1\;ml=1\;cm^3.
Milliliter och cm^3 är alltså samma sak. Därmed gäller att 200\;ml=200\;cm^3.
Vi får att 2 dl är lika med 200\;cm^3.
Titta på genomgången
För att förstå volym- och volymenheter på en djupare nivå kan du kolla på denna videon där det förklaras in i detalj.
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Omvandla 0,012 liter till milliliter.
Svarsalternativ 1.1: 0,12\;milliliter
Svarsalternativ 1.2: 1,2\;milliliter
Svarsalternativ 1.3: 12\;milliliter
Svarsalternativ 1.4: 120\;milliliter
Korrekt svar: 12\;milliliter
Fråga 2: Beräkna kubens volym. Svara i dm^3.
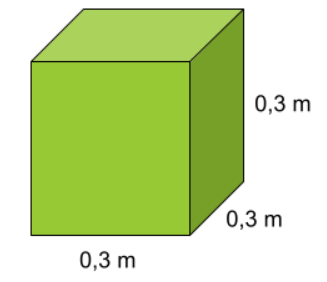
Svarsalternativ 2.1: 2,7\;dm^3
Svarsalternativ 2.2: 9\;dm^3
Svarsalternativ 2.3: 12\;dm^3
Svarsalternativ 2.4: 27\;dm^3
Korrekt svar: 27\;dm^3
Fråga 3: Omvandla 0,06\;dm^3 till centiliter.
Svarsalternativ 3.1: 6 centiliter
Svarsalternativ 3.2: 60 centiliter
Svarsalternativ 3.3: 600 centiliter
Svarsalternativ 3.4: 900 centiliter
Korrekt svar: 6 centiliter
Fredriks tips
Dubbelkolla enheterna

Vissa uppgifter där du beräknar volym kan ibland vara lite knepiga, särskilt när det gäller att hantera olika enheter. Se därför till att alltid dubbelkolla att alla sidor av formen är angivna i samma enhet. Därefter kan du beräkna basen och sedan även volymen för figuren. När du jämför olika volymer är det återigen viktigt att hålla koll på volymenheterna. Tänk på att när du konverterar mellan volymenheterna flyttar du decimaltecknet 3 steg. Ett användbart knep är att använda 3:an i till exempel cm^3 som en påminnelse för 3 steg!
Det kan lätt kännas lite krångligt när man börjar jobba med olika volymer men oroa dig inte! Med en studiecoach från Allakando blir det helt plötsligt mycket enklare att beräkna volym med olika volymenheter. Våra coacher har själva uppnått toppresultat i matematiken och hjälper dig gärna bemästra hur du räknar på volym!

Fredrik Fridlund, VD & Grundare
Har själv undervisat över 3 000 elever sedan 2007
Så hjälper Allakando dig till toppresultat i skolan

Mattehjälp för alla nivåer
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

